
기존 회전(오일러 회전/x,y,z각도회전)방식의 문제는 뭘까??
짐벌락 현상이 발생 -> 두 축이 겹치는 현상이 발생한다.
비행기를 예로 들어보자.
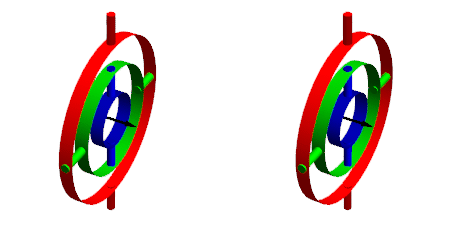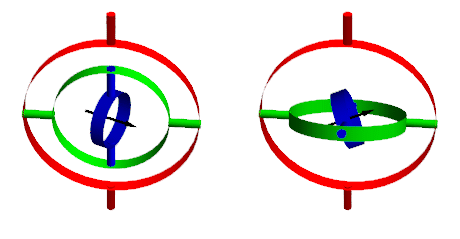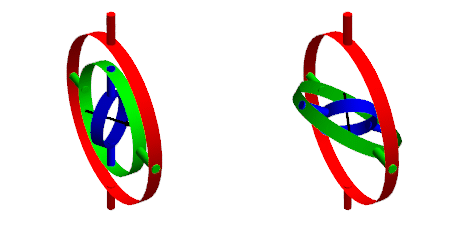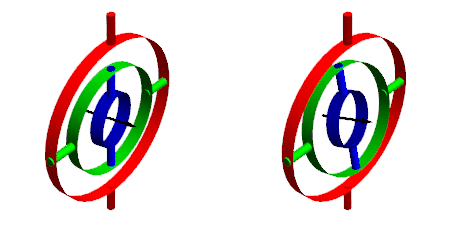
- 빨간링 - 비행기의 수직적인 시야 각도를 조절하는 링(위/아래)
- 파랑링 - 비행기의 수평적인 시야 각도를 조절하는 링(좌/우)
- 초록링 - 비행기의 날개 각도를 조정하는 링
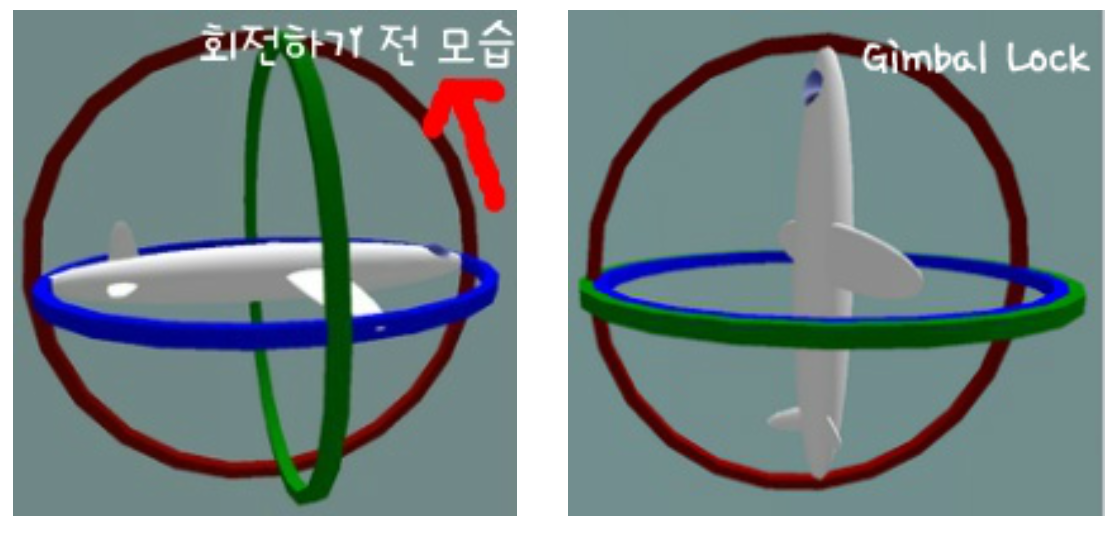
빨간링을 90도 회전시 파랑링과 초록링의 역할이 모두 초록링의 역할(비행기의 날개 각도를 조절)로 고정이 되어버린다.
예전설명)
만약 위의 그림에서
초록링을 먼저 한바퀴 회전시킨뒤 빨간링을 화살표 방향으로 90도 회전 시켰다면
초록링과 파랑링이 서로 겹쳐버리게 된다.
따라서 초록링과 파랑링은 모두 날개 각도를 조정하는 초록링의 원래 역할을 하게 된다.
파랑링의 역할이 없어지는 것이다.한 축이 기능을 잃는다는 것이 핵심이다.
복소수
z = a + bi
// 복소수 평면
(y)
|
| /|
| r / | r*sin(a)
| / |
| / |
|------------------ (x)
r*cos(a)
z = a + bi
i^2 = -1
|z| = |a+bi| = sqrt(a^2+b+2)
z^* = a-bi
// 덧셈
(a+bi) + (c+di) = (a+b) + i(b+d)
// 곱샘
(a+bi) * (c+di) = (ac - bd) + i(ad+bc)
z*z^* = a^2 + b^2 = |z|^2
그래서 복소수를 어디쓰나??
극좌표계의 경우 크기와 방향으로 각도를 표현할수 있다.
극좌표계를 이용하여 기존에 표현하던 각도를 다른 방법으로 표현해보자.
(y)
| (z)
| /|
| r / | r*sin(a)
| / |
| / |
|------------------ (x)
r*cos(a)
z1 = r1(cos(a) + i*sin(a))
z2 = r2(cos(b) + i*sin(b))
// 왠지는 모르겠지만 z1*z2을 해보고 싶다
z1*z2 = ???
= r1*r2(cos(a)cos(b) + i(cos(a)cos(b) + i(sin(a)sin(b) - sin(a)sin(b))))
= r1*r2(cos(a)cos(b) - sin(a)sin(b) + i(cos(a)sin(b) + sin(a)cos(b)))
= r1*r2(cos(a+b) + i(sin(a+b)))
z1이 2차원 벡터이고, z2가 단위 복소수(크기1)라면 그 결과는
크기가 z1의 크기에 z1 각도+z2 각도한 값이 나오게 된다. -> z1의 회전을 한 것이다.
즉, 복소수로 2D표현을 표현할 수 있고, 이제 3D회전을 어떻게 표현할까만 고민해 보면된다.